Mixed Integer and Hierarchical Design Spaces (Variables, Sampling and Context)

Mixed-discrete surrogate models need detailed information about the behavior of the design space (the input space), which you can specify using the design_space module. The design space definition module also supports specifying design space hierarchy including conditionally active design variables.

Design variables types

The following variable types are supported:

• Float: the variable can assume any real/continuous value between two bounds (inclusive)

• Integer: the variable can assume any integer value between two bounds (inclusive)

• Ordinal: the variable can assume any value from some set, order is relevant

• Categorical: the variable can assume any value from some set, order is not relevant

Integer, ordinal and categorical variables are all discrete variables, as they can only assume specific values from some set. The main differences between these types is the question whether distance and whether ordering matters:

• Integer: distance and order matters, e.g. the number of engines on an aircraft

• Ordinal: only order matters, e.g. steps in a process

• Categorical: neither distance nor order matters, e.g. different means for providing some functionality

More details can be found in [1] .

Variables are specified using the DesignVariable classes in smt.utils.design_space: - FloatVariable(lower_bound, upper_bound), upper should be greater than lower bound - IntegerVariable(lower_bound, upper_bound), bounds should be integers - OrdinalVariable(values), values is a list of int, float or str, encoded as integers from 0 to len(values)-1 - CategoricalVariable(values), same specification and encoding as ordinal

The design space is then defined from a list of design variables and implements sampling and correction interfaces:

import numpy as np

from smt.applications.mixed_integer import MixedIntegerSamplingMethod
from smt.sampling_methods import LHS
from smt.utils.design_space import (
    CategoricalVariable,
    DesignSpace,
    FloatVariable,
    IntegerVariable,
    OrdinalVariable,
)

ds = DesignSpace(
    [
        CategoricalVariable(
            ["A", "B"]
        ),  # x0 categorical: A or B; order is not relevant
        OrdinalVariable(
            ["C", "D", "E"]
        ),  # x1 ordinal: C, D or E; order is relevant
        IntegerVariable(
            0, 2
        ),  # x2 integer between 0 and 2 (inclusive): 0, 1, 2
        FloatVariable(0, 1),  # c3 continuous between 0 and 1
    ]
)

# Sample the design space
# Note: is_acting_sampled specifies for each design variable whether it is acting or not
ds.seed = 42
samp = MixedIntegerSamplingMethod(
    LHS, ds, criterion="ese", random_state=ds.seed
)
x_sampled, is_acting_sampled = samp(100, return_is_acting=True)

# Correct design vectors: round discrete variables, correct hierarchical variables
x_corr, is_acting = ds.correct_get_acting(
    np.array(
        [
            [0, 0, 2, 0.25],
            [0, 2, 1, 0.75],
        ]
    )
)
print(is_acting)

[[ True  True  True  True]
 [ True  True  True  True]]

Hierarchical variables

The design space definition uses the framework of Audet et al. [2] to manage both mixed-discrete variables and hierarchical variables. We distinguish dimensional (or meta) variables which are a special type of variables that may affect the dimension of the problem and decide if some other decreed variables are acting or non-acting.

Additionally, it is also possible to define value constraints that explicitly forbid two variables from having some values simultaneously or for a continuous variable to be greater than another. This can be useful for modeling incompatibility relationships: for example, engines can’t be installed on the back of the fuselage (vs on the wings) if a normal tail (vs T-tail) is selected. Note: this feature is only available if ConfigSpace has been installed: pip install smt[cs]

The hierarchy relationships are specified after instantiating the design space:

import numpy as np

from smt.applications.mixed_integer import (
    MixedIntegerKrigingModel,
    MixedIntegerSamplingMethod,
)
from smt.sampling_methods import LHS
from smt.surrogate_models import KRG, MixHrcKernelType, MixIntKernelType
from smt.utils.design_space import (
    CategoricalVariable,
    DesignSpace,
    FloatVariable,
    IntegerVariable,
    OrdinalVariable,
)

ds = DesignSpace(
    [
        CategoricalVariable(
            ["A", "B"]
        ),  # x0 categorical: A or B; order is not relevant
        OrdinalVariable(
            ["C", "D", "E"]
        ),  # x1 ordinal: C, D or E; order is relevant
        IntegerVariable(
            0, 2
        ),  # x2 integer between 0 and 2 (inclusive): 0, 1, 2
        FloatVariable(0, 1),  # c3 continuous between 0 and 1
    ]
)

# Declare that x1 is acting if x0 == A
ds.declare_decreed_var(decreed_var=1, meta_var=0, meta_value="A")

# Nested hierarchy is possible: activate x2 if x1 == C or D
# Note: only if ConfigSpace is installed! pip install smt[cs]
ds.declare_decreed_var(decreed_var=2, meta_var=1, meta_value=["C", "D"])

# It is also possible to explicitly forbid two values from occurring simultaneously
# Note: only if ConfigSpace is installed! pip install smt[cs]
ds.add_value_constraint(
    var1=0, value1="A", var2=2, value2=[0, 1]
)  # Forbid x0 == A && x2 == 0 or 1

# For quantitative variables, it is possible to specify order relation
ds.add_value_constraint(
    var1=2, value1="<", var2=3, value2=">"
)  # Prevent x2 < x3

# Sample the design space
# Note: is_acting_sampled specifies for each design variable whether it is acting or not
ds.seed = 42
samp = MixedIntegerSamplingMethod(
    LHS, ds, criterion="ese", random_state=ds.seed
)
Xt, is_acting_sampled = samp(100, return_is_acting=True)

rng = np.random.default_rng(42)
Yt = 4 * rng.random(100) - 2 + Xt[:, 0] + Xt[:, 1] - Xt[:, 2] - Xt[:, 3]
# Correct design vectors: round discrete variables, correct hierarchical variables
x_corr, is_acting = ds.correct_get_acting(
    np.array(
        [
            [0, 0, 2, 0.25],
            [0, 2, 1, 0.75],
            [1, 2, 1, 0.66],
        ]
    )
)

# Observe the hierarchical behavior:
assert np.all(
    is_acting
    == np.array(
        [
            [True, True, True, True],
            [
                True,
                True,
                False,
                True,
            ],  # x2 is not acting if x1 != C or D (0 or 1)
            [
                True,
                False,
                False,
                True,
            ],  # x1 is not acting if x0 != A, and x2 is not acting because x1 is not acting
        ]
    )
)
assert np.all(
    x_corr
    == np.array(
        [
            [0, 0, 2, 0.25],
            [0, 2, 0, 0.75],
            # x2 is not acting, so it is corrected ("imputed") to its non-acting value (0 for discrete vars)
            [1, 0, 0, 0.66],  # x1 and x2 are imputed
        ]
    )
)

sm = MixedIntegerKrigingModel(
    surrogate=KRG(
        design_space=ds,
        categorical_kernel=MixIntKernelType.HOMO_HSPHERE,
        hierarchical_kernel=MixHrcKernelType.ALG_KERNEL,
        theta0=[1e-2],
        hyper_opt="Cobyla",
        corr="abs_exp",
        n_start=5,
    ),
)
sm.set_training_values(Xt, Yt)
sm.train()
y_s = sm.predict_values(Xt)[:, 0]
pred_RMSE = np.linalg.norm(y_s - Yt) / len(Yt)

y_sv = sm.predict_variances(Xt)[:, 0]
_var_RMSE = np.linalg.norm(y_sv) / len(Yt)
assert pred_RMSE < 1e-7
print("Pred_RMSE", pred_RMSE)

self._sm = sm  # to be ignored: just used for automated test

___________________________________________________________________________

 Evaluation

      # eval points. : 100

   Predicting ...
   Predicting - done. Time (sec):  0.2882528

   Prediction time/pt. (sec) :  0.0028825

Pred_RMSE 4.0000324624835547e-13

Design space and variable class references

The DesignSpace class and design variable classes implement the relevant functionality.

class smt.utils.design_space.FloatVariable(lower: float, upper: float)

A continuous design variable, varying between its lower and upper bounds

Methods

get_typename

class smt.utils.design_space.IntegerVariable(lower: int, upper: int)

An integer variable that can take any integer value between the bounds (inclusive)

Methods

get_typename

class smt.utils.design_space.OrdinalVariable(values: List[int | float | str])

An ordinal variable that can take any of the given value, and where order between the values matters

Attributes:

lower

upper

Methods

get_typename

class smt.utils.design_space.CategoricalVariable(values: List[int | float | str])

A categorical variable that can take any of the given values, and where order does not matter

Attributes:

lower

n_values

upper

Methods

get_typename

class smt.utils.design_space.DesignSpace(design_variables: List[DesignVariable] | list | ndarray, random_state=None)

Class for defining a (hierarchical) design space by defining design variables, defining decreed variables (optional), and adding value constraints (optional).

Numerical bounds can be requested using get_num_bounds(). If needed, it is possible to get the legacy SMT < 2.0 xlimits format using get_x_limits().

Parameters:

design_variables: list[DesignVariable]

• The list of design variables: FloatVariable, IntegerVariable, OrdinalVariable, or CategoricalVariable

Examples

Instantiate the design space with all its design variables:

>>> from smt.utils.design_space import *
>>> ds = DesignSpace([
>>>     CategoricalVariable(['A', 'B']),  # x0 categorical: A or B; order is not relevant
>>>     OrdinalVariable(['C', 'D', 'E']),  # x1 ordinal: C, D or E; order is relevant
>>>     IntegerVariable(0, 2),  # x2 integer between 0 and 2 (inclusive): 0, 1, 2
>>>     FloatVariable(0, 1),  # c3 continuous between 0 and 1
>>> ])
>>> assert len(ds.design_variables) == 4

You can define decreed variables (conditional activation):

>>> ds.declare_decreed_var(decreed_var=1, meta_var=0, meta_value='A')  # Activate x1 if x0 == A

Decreed variables can be chained (however no cycles and no “diamonds” are supported): Note: only if ConfigSpace is installed! pip install smt[cs] >>> ds.declare_decreed_var(decreed_var=2, meta_var=1, meta_value=[‘C’, ‘D’]) # Activate x2 if x1 == C or D

If combinations of values between two variables are not allowed, this can be done using a value constraint: Note: only if ConfigSpace is installed! pip install smt[cs] >>> ds.add_value_constraint(var1=0, value1=’A’, var2=2, value2=[0, 1]) # Forbid x0 == A && x2 == 0 or 1

After defining everything correctly, you can then use the design space object to correct design vectors and get information about which design variables are acting:

>>> x_corr, is_acting = ds.correct_get_acting(np.array([
>>>     [0, 0, 2, .25],
>>>     [0, 2, 1, .75],
>>> ]))
>>> assert np.all(x_corr == np.array([
>>>     [0, 0, 2, .25],
>>>     [0, 2, 0, .75],
>>> ]))
>>> assert np.all(is_acting == np.array([
>>>     [True, True, True, True],
>>>     [True, True, False, True],  # x2 is not acting if x1 != C or D (0 or 1)
>>> ]))

It is also possible to randomly sample design vectors conforming to the constraints:

>>> x_sampled, is_acting_sampled = ds.sample_valid_x(100)

You can also instantiate a purely-continuous design space from bounds directly:

>>> continuous_design_space = DesignSpace([(0, 1), (0, 2), (.5, 5.5)])
>>> assert continuous_design_space.n_dv == 3

If needed, it is possible to get the legacy design space definition format:

>>> xlimits = ds.get_x_limits()
>>> cont_bounds = ds.get_num_bounds()
>>> unfolded_cont_bounds = ds.get_unfolded_num_bounds()

Attributes:

design_variables

is_all_cont

Whether or not the space is continuous

is_cat_mask

Boolean mask specifying for each design variable whether it is a categorical variable

is_conditionally_acting

Boolean mask specifying for each design variable whether it is conditionally acting (can be non-acting)

n_dv

Get the number of design variables

Methods

add_value_constraint(var1, value1, var2, value2)	Define a constraint where two variables cannot have the given values at the same time.
correct_get_acting(x)	Correct the given matrix of design vectors and return the corrected vectors and the is_acting matrix.
declare_decreed_var(decreed_var, meta_var, ...)	Define a conditional (decreed) variable to be active when the meta variable has (one of) the provided values.
decode_values(x[, i_dv])	Return decoded values: converts ordinal and categorical back to their original values.
sample_valid_x(n[, unfolded, random_state])	Sample n design vectors and additionally return the is_acting matrix.

add_value_constraint(var1: int, value1: int | str | List[str | int], var2: int, value2: int | str | List[str | int])

Define a constraint where two variables cannot have the given values at the same time.

Parameters:

var1: int

• Index of the first variable

value1: int | str | list[int|str]

• Value or values that the first variable is checked against

var2: int

• Index of the second variable

value2: int | str | list[int|str]

• Value or values that the second variable is checked against

correct_get_acting(x: ndarray) → Tuple[ndarray, ndarray]

Correct the given matrix of design vectors and return the corrected vectors and the is_acting matrix. It is automatically detected whether input is provided in unfolded space or not.

Parameters:

x: np.ndarray [n_obs, dim]

• Input variables

Returns:

x_corrected: np.ndarray [n_obs, dim]

• Corrected and imputed input variables

is_acting: np.ndarray [n_obs, dim]

• Boolean matrix specifying for each variable whether it is acting or non-acting

declare_decreed_var(decreed_var: int, meta_var: int, meta_value: int | str | List[str | int])

Define a conditional (decreed) variable to be active when the meta variable has (one of) the provided values.

Parameters:

decreed_var: int

• Index of the conditional variable (the variable that is conditionally active)

meta_var: int

• Index of the meta variable (the variable that determines whether the conditional var is active)

meta_value: int | str | list[int|str]

• The value or list of values that the meta variable can have to activate the decreed var

decode_values(x: ndarray, i_dv: int = None) → List[str | int | float | list]

Return decoded values: converts ordinal and categorical back to their original values.

If i_dv is given, decoding is done for one specific design variable only. If i_dv=None, decoding will be done for all design variables: 1d input is interpreted as a design vector, 2d input is interpreted as a set of design vectors.

property is_all_cont: bool

Whether or not the space is continuous

property is_cat_mask: ndarray

Boolean mask specifying for each design variable whether it is a categorical variable

property is_conditionally_acting: ndarray

Boolean mask specifying for each design variable whether it is conditionally acting (can be non-acting)

property n_dv: int

Get the number of design variables

sample_valid_x(n: int, unfolded=False, random_state=None) → Tuple[ndarray, ndarray]

Sample n design vectors and additionally return the is_acting matrix.

Parameters:

n: int

• Number of samples to generate

unfolded: bool

• Whether to return the samples in unfolded space (each categorical level gets its own dimension)

Returns:

x: np.ndarray [n, dim]

• Valid design vectors

is_acting: np.ndarray [n, dim]

• Boolean matrix specifying for each variable whether it is acting or non-acting

Example of sampling a mixed-discrete design space

import matplotlib.pyplot as plt
import numpy as np
from matplotlib import colors

from smt.applications.mixed_integer import MixedIntegerSamplingMethod
from smt.sampling_methods import LHS
from smt.utils.design_space import (
    CategoricalVariable,
    DesignSpace,
    FloatVariable,
)

float_var = FloatVariable(0, 4)
cat_var = CategoricalVariable(["blue", "red"])

design_space = DesignSpace(
    [
        float_var,
        cat_var,
    ]
)

num = 40
design_space.seed = 42
samp = MixedIntegerSamplingMethod(
    LHS, design_space, criterion="ese", random_state=design_space.seed
)
x, x_is_acting = samp(num, return_is_acting=True)

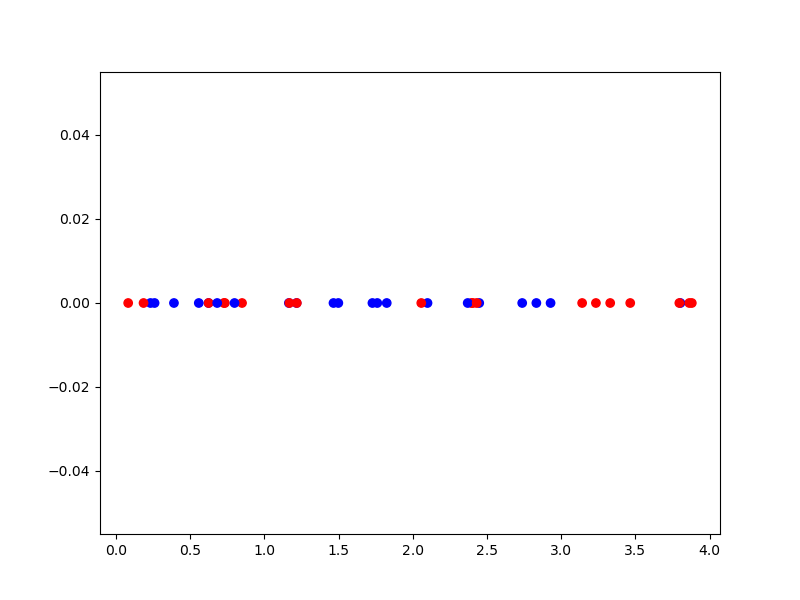
cmap = colors.ListedColormap(cat_var.values)
plt.scatter(x[:, 0], np.zeros(num), c=x[:, 1], cmap=cmap)
plt.show()

Mixed integer context

The MixedIntegerContext class helps the user to use mixed integer sampling methods and surrogate models consistently by acting as a factory for those objects given a x specification: (xtypes, xlimits).

class smt.applications.mixed_integer.MixedIntegerContext(design_space, work_in_folded_space=True)

Class which acts as sampling method and surrogate model factory to handle integer and categorical variables consistently.

Attributes:

design_space

Methods

build_kriging_model(surrogate)	Build MixedIntegerKrigingModel from given SMT surrogate model.
build_sampling_method([random_state])	Build Mixed Integer LHS ESE sampler.
build_surrogate_model(surrogate)	Build MixedIntegerKrigingModel from given SMT surrogate model.
get_unfolded_dimension()	Returns x dimension (int) taking into account unfolded categorical features
get_unfolded_xlimits()	Returns relaxed xlimits Each level of an enumerate gives a new continuous dimension in [0, 1].

MixedIntegerContext.__init__(design_space, work_in_folded_space=True)

Parameters:

design_space: BaseDesignSpace

the design space definition (includes mixed-discrete and/or hierarchical specifications)

work_in_folded_space: bool

whether x data are in given in folded space (enum indexes) or not (enum masks)

MixedIntegerContext.build_sampling_method(random_state=None)

Build Mixed Integer LHS ESE sampler.

MixedIntegerContext.build_surrogate_model(surrogate)

Build MixedIntegerKrigingModel from given SMT surrogate model.

Example of mixed integer context usage

import matplotlib.pyplot as plt

from smt.applications.mixed_integer import MixedIntegerContext
from smt.surrogate_models import KRG
from smt.utils.design_space import (
    CategoricalVariable,
    DesignSpace,
    FloatVariable,
    IntegerVariable,
)

design_space = DesignSpace(
    [
        IntegerVariable(0, 5),
        FloatVariable(0.0, 4.0),
        CategoricalVariable(["blue", "red", "green", "yellow"]),
    ]
)

def ftest(x):
    return (x[:, 0] * x[:, 0] + x[:, 1] * x[:, 1]) * (x[:, 2] + 1)

# Helper class for creating surrogate models
mi_context = MixedIntegerContext(design_space)

# DOE for training
sampler = mi_context.build_sampling_method()

num = mi_context.get_unfolded_dimension() * 5
print("DOE point nb = {}".format(num))
xt = sampler(num)
yt = ftest(xt)

# Surrogate
sm = mi_context.build_kriging_model(KRG(hyper_opt="Cobyla"))
sm.set_training_values(xt, yt)
sm.train()

# DOE for validation
xv = sampler(50)
yv = ftest(xv)
yp = sm.predict_values(xv)

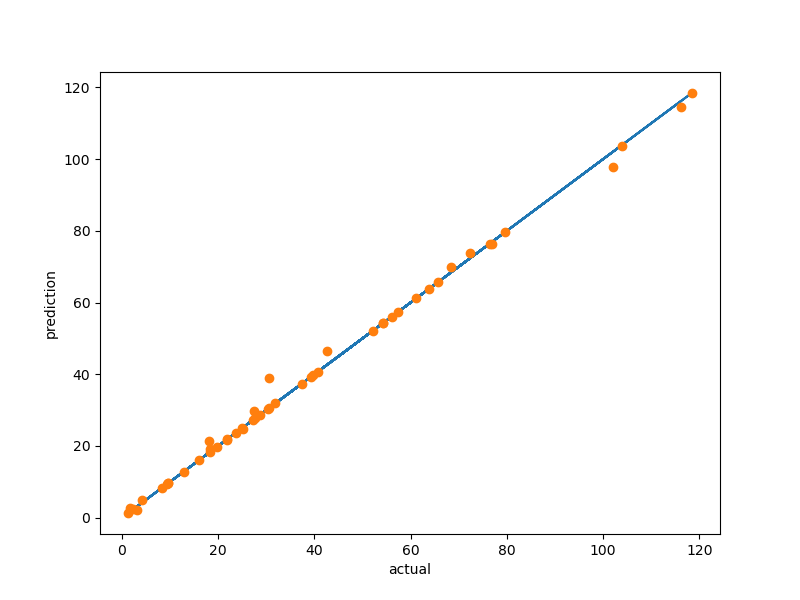
plt.plot(yv, yv)
plt.plot(yv, yp, "o")
plt.xlabel("actual")
plt.ylabel("prediction")

plt.show()

DOE point nb = 30
___________________________________________________________________________

 Evaluation

      # eval points. : 50

   Predicting ...
   Predicting - done. Time (sec):  0.0114698

   Prediction time/pt. (sec) :  0.0002294

References

[1]

Saves, P. and Diouane, Y. and Bartoli, N. and Lefebvre, T. and Morlier, J. (2022). A general square exponential kernel to handle mixed-categorical variables for Gaussian process. AIAA Aviation 2022 Forum.

[2]

Audet, C., Hallé-Hannan, E. and Le Digabel, S. A General Mathematical Framework for Constrained Mixed-variable Blackbox Optimization Problems with Meta and Categorical Variables. Oper. Res. Forum 4, 12 (2023).