1-D step-like data set¶
import numpy as np
def get_one_d_step():
xt = np.array(
[
0.0000,
0.4000,
0.6000,
0.7000,
0.7500,
0.7750,
0.8000,
0.8500,
0.8750,
0.9000,
0.9250,
0.9500,
0.9750,
1.0000,
1.0250,
1.0500,
1.1000,
1.2000,
1.3000,
1.4000,
1.6000,
1.8000,
2.0000,
],
dtype=np.float64,
)
yt = np.array(
[
0.0130,
0.0130,
0.0130,
0.0130,
0.0130,
0.0130,
0.0130,
0.0132,
0.0135,
0.0140,
0.0162,
0.0230,
0.0275,
0.0310,
0.0344,
0.0366,
0.0396,
0.0410,
0.0403,
0.0390,
0.0360,
0.0350,
0.0345,
],
dtype=np.float64,
)
xlimits = np.array([[0.0, 2.0]])
return xt, yt, xlimits
def plot_one_d_step(xt, yt, limits, interp):
import numpy as np
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
num = 500
x = np.linspace(0.0, 2.0, num)
y = interp.predict_values(x)[:, 0]
plt.plot(x, y)
plt.plot(xt, yt, "o")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
RMTB¶
from smt.surrogate_models import RMTB
from smt.examples.one_D_step.one_D_step import get_one_d_step, plot_one_d_step
xt, yt, xlimits = get_one_d_step()
interp = RMTB(
num_ctrl_pts=100,
xlimits=xlimits,
nonlinear_maxiter=20,
solver_tolerance=1e-16,
energy_weight=1e-14,
regularization_weight=0.0,
)
interp.set_training_values(xt, yt)
interp.train()
plot_one_d_step(xt, yt, xlimits, interp)
___________________________________________________________________________
RMTB
___________________________________________________________________________
Problem size
# training points. : 23
___________________________________________________________________________
Training
Training ...
Pre-computing matrices ...
Computing dof2coeff ...
Computing dof2coeff - done. Time (sec): 0.0000010
Initializing Hessian ...
Initializing Hessian - done. Time (sec): 0.0001290
Computing energy terms ...
Computing energy terms - done. Time (sec): 0.0003998
Computing approximation terms ...
Computing approximation terms - done. Time (sec): 0.0001318
Pre-computing matrices - done. Time (sec): 0.0006788
Solving for degrees of freedom ...
Solving initial startup problem (n=100) ...
Solving for output 0 ...
Iteration (num., iy, grad. norm, func.) : 0 0 1.032652876e-01 8.436300000e-03
Iteration (num., iy, grad. norm, func.) : 0 0 6.635904983e-08 2.327261878e-13
Solving for output 0 - done. Time (sec): 0.0021889
Solving initial startup problem (n=100) - done. Time (sec): 0.0022101
Solving nonlinear problem (n=100) ...
Solving for output 0 ...
Iteration (num., iy, grad. norm, func.) : 0 0 1.444402121e-11 2.288885480e-13
Iteration (num., iy, grad. norm, func.) : 0 0 1.272709096e-11 2.260792226e-13
Iteration (num., iy, grad. norm, func.) : 1 0 4.504959172e-10 1.377502458e-13
Iteration (num., iy, grad. norm, func.) : 2 0 3.647939893e-10 1.078764231e-13
Iteration (num., iy, grad. norm, func.) : 3 0 1.075871896e-10 2.732387288e-14
Iteration (num., iy, grad. norm, func.) : 4 0 3.126947171e-11 1.193386752e-14
Iteration (num., iy, grad. norm, func.) : 5 0 3.030871550e-11 1.180224451e-14
Iteration (num., iy, grad. norm, func.) : 6 0 8.633161747e-12 9.023771851e-15
Iteration (num., iy, grad. norm, func.) : 7 0 2.095321878e-12 8.515252595e-15
Iteration (num., iy, grad. norm, func.) : 8 0 3.455129224e-13 8.461652833e-15
Iteration (num., iy, grad. norm, func.) : 9 0 1.829996952e-13 8.457807423e-15
Iteration (num., iy, grad. norm, func.) : 10 0 1.798377797e-14 8.453841725e-15
Iteration (num., iy, grad. norm, func.) : 11 0 2.181386654e-14 8.453757638e-15
Iteration (num., iy, grad. norm, func.) : 12 0 7.572293809e-15 8.453468374e-15
Iteration (num., iy, grad. norm, func.) : 13 0 1.726280069e-14 8.453421611e-15
Iteration (num., iy, grad. norm, func.) : 14 0 5.403084873e-15 8.453331934e-15
Iteration (num., iy, grad. norm, func.) : 15 0 2.173878029e-15 8.453284013e-15
Iteration (num., iy, grad. norm, func.) : 16 0 3.711317412e-16 8.453271707e-15
Iteration (num., iy, grad. norm, func.) : 17 0 4.061922728e-16 8.453271656e-15
Iteration (num., iy, grad. norm, func.) : 18 0 5.023861547e-16 8.453271235e-15
Iteration (num., iy, grad. norm, func.) : 19 0 2.956920126e-16 8.453270899e-15
Solving for output 0 - done. Time (sec): 0.0415142
Solving nonlinear problem (n=100) - done. Time (sec): 0.0415301
Solving for degrees of freedom - done. Time (sec): 0.0437579
Training - done. Time (sec): 0.0445950
___________________________________________________________________________
Evaluation
# eval points. : 500
Predicting ...
Predicting - done. Time (sec): 0.0001390
Prediction time/pt. (sec) : 0.0000003
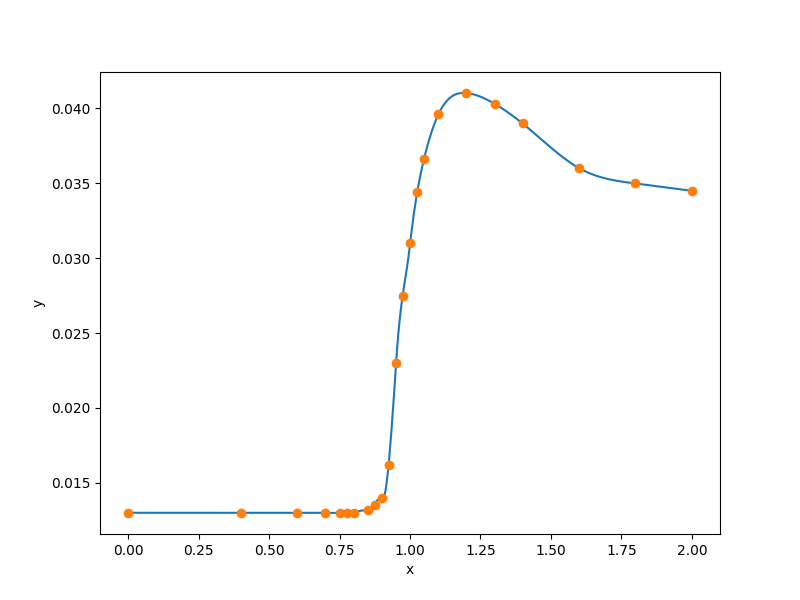
RMTC¶
from smt.surrogate_models import RMTC
from smt.examples.one_D_step.one_D_step import get_one_d_step, plot_one_d_step
xt, yt, xlimits = get_one_d_step()
interp = RMTC(
num_elements=40,
xlimits=xlimits,
nonlinear_maxiter=20,
solver_tolerance=1e-16,
energy_weight=1e-14,
regularization_weight=0.0,
)
interp.set_training_values(xt, yt)
interp.train()
plot_one_d_step(xt, yt, xlimits, interp)
___________________________________________________________________________
RMTC
___________________________________________________________________________
Problem size
# training points. : 23
___________________________________________________________________________
Training
Training ...
Pre-computing matrices ...
Computing dof2coeff ...
Computing dof2coeff - done. Time (sec): 0.0002601
Initializing Hessian ...
Initializing Hessian - done. Time (sec): 0.0001040
Computing energy terms ...
Computing energy terms - done. Time (sec): 0.0003772
Computing approximation terms ...
Computing approximation terms - done. Time (sec): 0.0001659
Pre-computing matrices - done. Time (sec): 0.0009229
Solving for degrees of freedom ...
Solving initial startup problem (n=82) ...
Solving for output 0 ...
Iteration (num., iy, grad. norm, func.) : 0 0 1.470849329e-01 8.436300000e-03
Iteration (num., iy, grad. norm, func.) : 0 0 1.651391055e-09 2.493585990e-14
Solving for output 0 - done. Time (sec): 0.0020990
Solving initial startup problem (n=82) - done. Time (sec): 0.0021172
Solving nonlinear problem (n=82) ...
Solving for output 0 ...
Iteration (num., iy, grad. norm, func.) : 0 0 7.483916438e-12 2.493485504e-14
Iteration (num., iy, grad. norm, func.) : 0 0 9.032434603e-12 2.483123292e-14
Iteration (num., iy, grad. norm, func.) : 1 0 8.700736238e-11 2.391083256e-14
Iteration (num., iy, grad. norm, func.) : 2 0 4.235547668e-11 1.707888753e-14
Iteration (num., iy, grad. norm, func.) : 3 0 3.958092022e-11 1.662286479e-14
Iteration (num., iy, grad. norm, func.) : 4 0 2.726635798e-11 1.355247914e-14
Iteration (num., iy, grad. norm, func.) : 5 0 7.382891532e-12 1.137415853e-14
Iteration (num., iy, grad. norm, func.) : 6 0 1.394907606e-12 1.111064598e-14
Iteration (num., iy, grad. norm, func.) : 7 0 7.550198607e-13 1.109901845e-14
Iteration (num., iy, grad. norm, func.) : 8 0 9.984178597e-14 1.109058891e-14
Iteration (num., iy, grad. norm, func.) : 9 0 2.997183844e-14 1.108964247e-14
Iteration (num., iy, grad. norm, func.) : 10 0 7.829794250e-15 1.108943566e-14
Iteration (num., iy, grad. norm, func.) : 11 0 1.806946920e-15 1.108940737e-14
Iteration (num., iy, grad. norm, func.) : 12 0 4.529794331e-16 1.108940402e-14
Iteration (num., iy, grad. norm, func.) : 13 0 1.259856346e-16 1.108940349e-14
Iteration (num., iy, grad. norm, func.) : 14 0 3.400896486e-17 1.108940340e-14
Solving for output 0 - done. Time (sec): 0.0308747
Solving nonlinear problem (n=82) - done. Time (sec): 0.0308878
Solving for degrees of freedom - done. Time (sec): 0.0330250
Training - done. Time (sec): 0.0341151
___________________________________________________________________________
Evaluation
# eval points. : 500
Predicting ...
Predicting - done. Time (sec): 0.0001161
Prediction time/pt. (sec) : 0.0000002