Branin function¶
\[f(x) = (x_2 - \frac{5.1}{4\pi^2}x_1^{2} + \frac{5}{\pi}x_1 - 6)^2 + 10(1-\frac{1}{8\pi})\cos(x_1) + 10,\]
where \(x = (x_1, x_2)\) with \(-5\leq x_1 \leq 10, 0 \leq x_2 \leq 15\)
The Branin function has three global minima:
\(f(x^*) = 0.397887\), at \(x^* = (-\pi, 12.275), (\pi, 2.275)\) and \((9.42478, 2.475)\)
Usage¶
import numpy as np
import matplotlib.pyplot as plt
from smt.problems import Branin
ndim = 2
problem = Branin(ndim=ndim)
num = 100
x = np.ones((num, ndim))
x[:, 0] = np.linspace(-5.0, 10.0, num)
x[:, 1] = np.linspace(0.0, 15.0, num)
y = problem(x)
yd = np.empty((num, ndim))
for i in range(ndim):
yd[:, i] = problem(x, kx=i).flatten()
print(y.shape)
print(yd.shape)
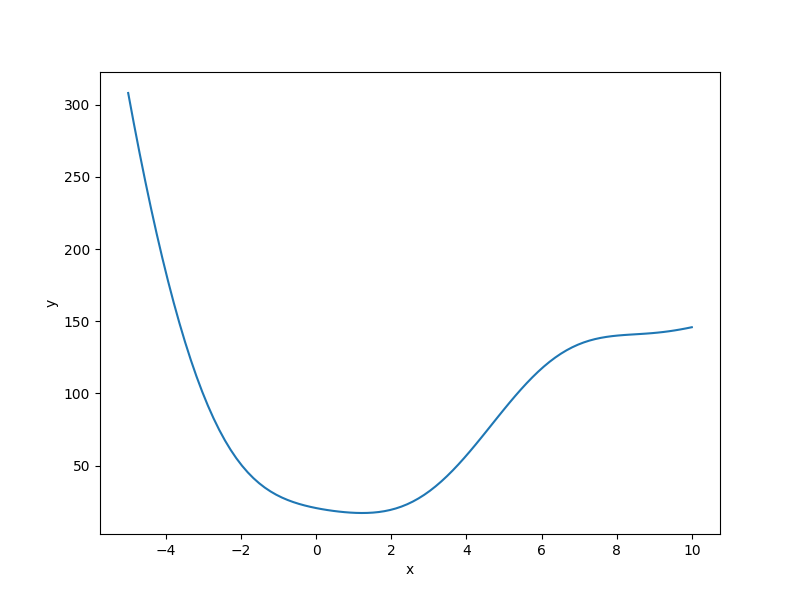
plt.plot(x[:, 0], y[:, 0])
plt.xlabel("x")
plt.ylabel("y")
plt.show()
(100, 1)
(100, 2)
Options¶
Option |
Default |
Acceptable values |
Acceptable types |
Description |
|---|---|---|---|---|
ndim |
2 |
[2] |
[‘int’] |
|
return_complex |
False |
None |
[‘bool’] |
|
name |
Branin |
None |
[‘str’] |