Torsion vibration function

\[\frac{1}{2\pi}\sqrt{\frac{-b-\sqrt{b^2-4ac}}{2a}},\]

where \(K_i=\frac{\pi G_id_i}{32L_i},\quad M_j=\frac{\rho_j \pi t_jD_j}{4g},\quad J_j=0.5M_j\frac{D_j}{2},\quad a = 1,\quad b=-\left(\frac{K_1+K2}{J_1}+\frac{K_2+K3}{J_2}\right),\quad c=\frac{K_1K_2+K_2K_3+K_3K_1}{J_1J_2},\quad \text{for}\quad d_1\in [1.8,2.2],\quad L_1\in[9,11],\quad G_1\in [105300000,128700000],\) \(d_2\in [1.638,2.002],\quad L_2\in[10.8,13.2],\quad G_2\in[5580000,6820000],\quad d_3\in[2.025,2.475],\quad L_3\in[7.2,8.8],\quad G_3\in[3510000,4290000],\quad D_1\in[10.8,13.2],\quad t_1\in[2.7,3.3],\) \(\rho_1\in[0.252,0.308], \quad D_2\in[12.6,15.4],\quad t_2\in[3.6,4.4],\quad\rho_1\in[0.09,0.11].\)

Usage

import numpy as np
import matplotlib.pyplot as plt

from smt.problems import TorsionVibration

ndim = 15
problem = TorsionVibration(ndim=ndim)

num = 100
x = np.ones((num, ndim))
for i in range(ndim):
    x[:, i] = 0.5 * (problem.xlimits[i, 0] + problem.xlimits[i, 1])
x[:, 0] = np.linspace(1.8, 2.2, num)
y = problem(x)

yd = np.empty((num, ndim))
for i in range(ndim):
    yd[:, i] = problem(x, kx=i).flatten()

print(y.shape)
print(yd.shape)

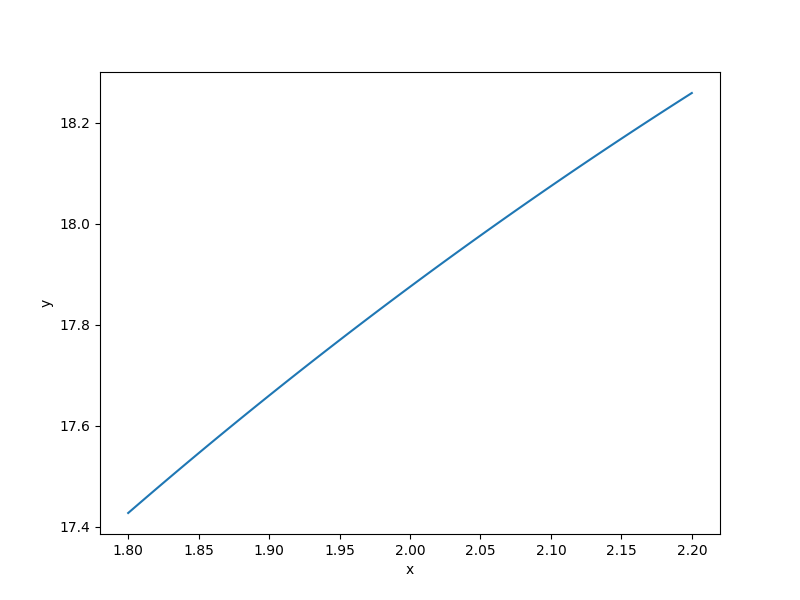
plt.plot(x[:, 0], y[:, 0])
plt.xlabel("x")
plt.ylabel("y")
plt.show()

(100, 1)
(100, 15)

Options

List of options

Option	Default	Acceptable values	Acceptable types	Description
ndim	1	None	[‘int’]
return_complex	False	None	[‘bool’]
name	TorsionVibration	None	[‘str’]
use_FD	False	None	[‘bool’]