Benchmarking problems

SMT contains a library of analytical and engineering problems to be used for benchmarking purposes. These are listed below.

• Sphere function
• Branin function
• Lp norm function
• Rosenbrock function
• Tensor-product function
• Cantilever beam function
• Mixed cantilever beam function
• Multi-layer perceptron
• Robot arm function
• Torsion vibration function
• Water flow function
• Welded beam function
• Wing weight function

Usage

import matplotlib.pyplot as plt
import numpy as np

from smt.problems import Sphere

ndim = 2
problem = Sphere(ndim=ndim)

num = 100
x = np.ones((num, ndim))
x[:, 0] = np.linspace(-10, 10.0, num)
x[:, 1] = 0.0
y = problem(x)

yd = np.empty((num, ndim))
for i in range(ndim):
    yd[:, i] = problem(x, kx=i).flatten()

print(y.shape)
print(yd.shape)

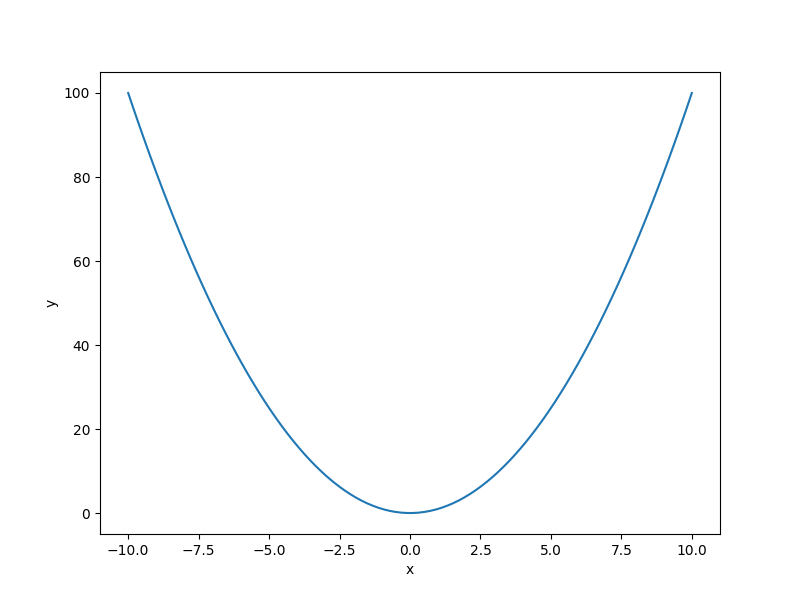
plt.plot(x[:, 0], y[:, 0])
plt.xlabel("x")
plt.ylabel("y")
plt.show()

(100, 1)
(100, 2)

Problem class API

class smt.problems.problem.Problem(**kwargs)

Attributes:

design_space

Gets the design space definitions as an instance of BaseDesignSpace

Methods

__call__(x[, kx])

Evaluate the function.

sample

__init__(**kwargs)

Constructor where values of options can be passed in.

For the list of options, see the documentation for the problem being used.

Parameters:

**kwargsnamed arguments

Set of options that can be optionally set; each option must have been declared.

Examples

>>> from smt.problems import Sphere
>>> prob = Sphere(ndim=3)

__call__(x: ndarray, kx: int | None = None) → ndarray

Evaluate the function. The input vectors might be corrected if it is a hierarchical design space. You can get the corrected x and information about which variables are acting from: problem.eval_x and problem.eval_is_acting

Parameters:

xndarray[n, nx] or ndarray[n]

Evaluation points where n is the number of evaluation points.

kxint or None

Index of derivative (0-based) to return values with respect to. None means return function value rather than derivative.

Returns:

ndarray[n, 1]

Functions values if kx=None or derivative values if kx is an int.