Regularized minimal-energy tensor-product splines¶
Regularized minimal-energy tensor-product splines (RMTS) is a type of surrogate model for low-dimensional problems with large datasets and where fast prediction is desired. The underlying mathematical functions are tensor-product splines, which limits RMTS to up to 4-D problems, or 5-D problems in certain cases. On the other hand, tensor-product splines enable a very fast prediction time that does not increase with the number of training points. Unlike other methods like Kriging and radial basis functions, RMTS is not susceptible to numerical issues when there is a large number of training points or when there are points that are too close together.
The prediction equation for RMTS is
where \(\mathbf{x} \in \mathbb{R}^{nx}\) is the prediction input vector, \(y \in \mathbb{R}\) is the prediction output, \(\mathbf{w} \in \mathbb{R}^{nw}\) is the vector of spline coefficients, and \(\mathbf{F}(\mathbf{x}) \in \mathbb{R}^{nw}\) is the vector mapping the spline coefficients to the prediction output.
RMTS computes the coefficients of the splines, \(\mathbf{w}\), by solving an energy minimization problem subject to the conditions that the splines pass through the training points. This is formulated as an unconstrained optimization problem where the objective function consists of a term containing the second derivatives of the splines, another term representing the approximation error for the training points, and another term for regularization:
where \(\mathbf{xt}_i \in \mathbb{R}^{nx}\) is the input vector for the \(i\) th training point, \(yt_i \in \mathbb{R}\) is the output value for the \(i\) th training point, \(\mathbf{H} \in \mathbb{R}^{nw \times nw}\) is the matrix containing the second derivatives, \(\mathbf{F}(\mathbf{xt}_i) \in \mathbb{R}^{nw}\) is the vector mapping the spline coefficients to the \(i\) th training output, and \(\alpha\) and \(\beta\) are regularization coefficients.
In problems with a large number of training points relative to the number of spline coefficients, the energy minimization term is not necessary; this term can be zero-ed by setting the reg_cons option to zero. In problems with a small dataset, the energy minimization is necessary. When the true function has high curvature, the energy minimization can be counterproductive in the regions of high curvature. This can be addressed by increasing the quadratic approximation term to one of higher order, and using Newton’s method to solve the nonlinear system that results. The nonlinear formulation is given by
where \(p\) is the order given by the approx_order option.
The number of Newton iterations can be specified via the nonlinear_maxiter option.
RMTS is implemented in SMT with two choices of splines:
1. B-splines (RMTB): RMTB uses B-splines with a uniform knot vector in each dimension. The number of B-spline control points and the B-spline order in each dimension are options that trade off efficiency and precision of the interpolant.
2. Cubic Hermite splines (RMTC): RMTC divides the domain into tensor-product cubic elements. For adjacent elements, the values and derivatives are continuous. The number of elements in each dimension is an option that trades off efficiency and precision.
In general, RMTB is the better choice when training time is the most important, while RMTC is the better choice when accuracy of the interpolant is the most important. More details of these methods are given in [1].
Usage (RMTB)¶
import numpy as np
import matplotlib.pyplot as plt
from smt.surrogate_models import RMTB
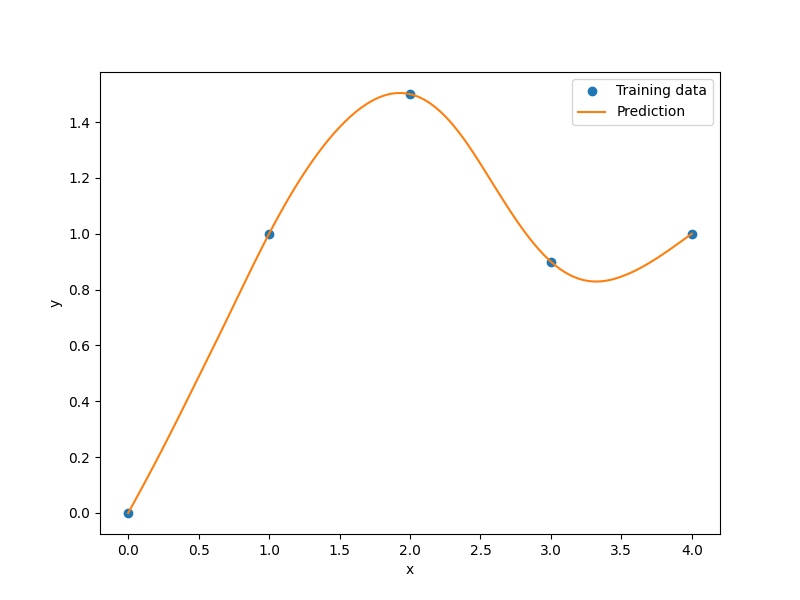
xt = np.array([0.0, 1.0, 2.0, 3.0, 4.0])
yt = np.array([0.0, 1.0, 1.5, 0.9, 1.0])
xlimits = np.array([[0.0, 4.0]])
sm = RMTB(
xlimits=xlimits,
order=4,
num_ctrl_pts=20,
energy_weight=1e-15,
regularization_weight=0.0,
)
sm.set_training_values(xt, yt)
sm.train()
num = 100
x = np.linspace(0.0, 4.0, num)
y = sm.predict_values(x)
plt.plot(xt, yt, "o")
plt.plot(x, y)
plt.xlabel("x")
plt.ylabel("y")
plt.legend(["Training data", "Prediction"])
plt.show()
___________________________________________________________________________
RMTB
___________________________________________________________________________
Problem size
# training points. : 5
___________________________________________________________________________
Training
Training ...
Pre-computing matrices ...
Computing dof2coeff ...
Computing dof2coeff - done. Time (sec): 0.0000007
Initializing Hessian ...
Initializing Hessian - done. Time (sec): 0.0001690
Computing energy terms ...
Computing energy terms - done. Time (sec): 0.0003760
Computing approximation terms ...
Computing approximation terms - done. Time (sec): 0.0001290
Pre-computing matrices - done. Time (sec): 0.0006931
Solving for degrees of freedom ...
Solving initial startup problem (n=20) ...
Solving for output 0 ...
Iteration (num., iy, grad. norm, func.) : 0 0 1.549745600e+00 2.530000000e+00
Iteration (num., iy, grad. norm, func.) : 0 0 1.698247986e-15 4.462619163e-16
Solving for output 0 - done. Time (sec): 0.0010281
Solving initial startup problem (n=20) - done. Time (sec): 0.0010440
Solving nonlinear problem (n=20) ...
Solving for output 0 ...
Iteration (num., iy, grad. norm, func.) : 0 0 1.532066659e-15 4.462619163e-16
Solving for output 0 - done. Time (sec): 0.0000570
Solving nonlinear problem (n=20) - done. Time (sec): 0.0000751
Solving for degrees of freedom - done. Time (sec): 0.0011392
Training - done. Time (sec): 0.0019877
___________________________________________________________________________
Evaluation
# eval points. : 100
Predicting ...
Predicting - done. Time (sec): 0.0000970
Prediction time/pt. (sec) : 0.0000010
Usage (RMTC)¶
import numpy as np
import matplotlib.pyplot as plt
from smt.surrogate_models import RMTC
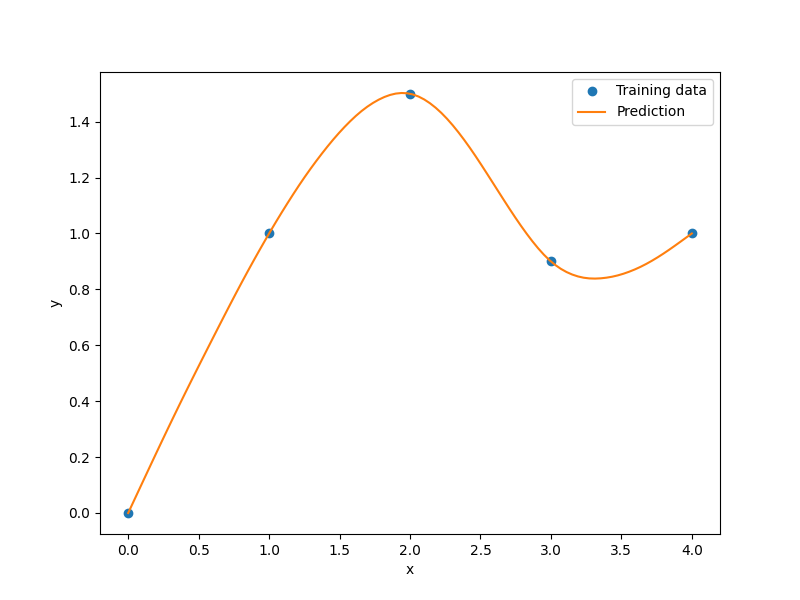
xt = np.array([0.0, 1.0, 2.0, 3.0, 4.0])
yt = np.array([0.0, 1.0, 1.5, 0.9, 1.0])
xlimits = np.array([[0.0, 4.0]])
sm = RMTC(
xlimits=xlimits,
num_elements=20,
energy_weight=1e-15,
regularization_weight=0.0,
)
sm.set_training_values(xt, yt)
sm.train()
num = 100
x = np.linspace(0.0, 4.0, num)
y = sm.predict_values(x)
plt.plot(xt, yt, "o")
plt.plot(x, y)
plt.xlabel("x")
plt.ylabel("y")
plt.legend(["Training data", "Prediction"])
plt.show()
___________________________________________________________________________
RMTC
___________________________________________________________________________
Problem size
# training points. : 5
___________________________________________________________________________
Training
Training ...
Pre-computing matrices ...
Computing dof2coeff ...
Computing dof2coeff - done. Time (sec): 0.0002878
Initializing Hessian ...
Initializing Hessian - done. Time (sec): 0.0001020
Computing energy terms ...
Computing energy terms - done. Time (sec): 0.0003712
Computing approximation terms ...
Computing approximation terms - done. Time (sec): 0.0001543
Pre-computing matrices - done. Time (sec): 0.0009301
Solving for degrees of freedom ...
Solving initial startup problem (n=42) ...
Solving for output 0 ...
Iteration (num., iy, grad. norm, func.) : 0 0 2.249444376e+00 2.530000000e+00
Iteration (num., iy, grad. norm, func.) : 0 0 2.079822643e-15 4.346868680e-16
Solving for output 0 - done. Time (sec): 0.0012138
Solving initial startup problem (n=42) - done. Time (sec): 0.0012312
Solving nonlinear problem (n=42) ...
Solving for output 0 ...
Iteration (num., iy, grad. norm, func.) : 0 0 2.956393318e-15 4.346868680e-16
Solving for output 0 - done. Time (sec): 0.0000536
Solving nonlinear problem (n=42) - done. Time (sec): 0.0000660
Solving for degrees of freedom - done. Time (sec): 0.0013151
Training - done. Time (sec): 0.0023849
___________________________________________________________________________
Evaluation
# eval points. : 100
Predicting ...
Predicting - done. Time (sec): 0.0000930
Prediction time/pt. (sec) : 0.0000009
Options (RMTB)¶
Option |
Default |
Acceptable values |
Acceptable types |
Description |
|---|---|---|---|---|
print_global |
True |
None |
[‘bool’] |
Global print toggle. If False, all printing is suppressed |
print_training |
True |
None |
[‘bool’] |
Whether to print training information |
print_prediction |
True |
None |
[‘bool’] |
Whether to print prediction information |
print_problem |
True |
None |
[‘bool’] |
Whether to print problem information |
print_solver |
True |
None |
[‘bool’] |
Whether to print solver information |
xlimits |
None |
None |
[‘ndarray’] |
Lower/upper bounds in each dimension - ndarray [nx, 2] |
smoothness |
1.0 |
None |
[‘Integral’, ‘float’, ‘tuple’, ‘list’, ‘ndarray’] |
Smoothness parameter in each dimension - length nx. None implies uniform |
regularization_weight |
1e-14 |
None |
[‘Integral’, ‘float’] |
Weight of the term penalizing the norm of the spline coefficients. This is useful as an alternative to energy minimization when energy minimization makes the training time too long. |
energy_weight |
0.0001 |
None |
[‘Integral’, ‘float’] |
The weight of the energy minimization terms |
extrapolate |
False |
None |
[‘bool’] |
Whether to perform linear extrapolation for external evaluation points |
min_energy |
True |
None |
[‘bool’] |
Whether to perform energy minimization |
approx_order |
4 |
None |
[‘Integral’] |
Exponent in the approximation term |
solver |
krylov |
[‘krylov-dense’, ‘dense-lu’, ‘dense-chol’, ‘lu’, ‘ilu’, ‘krylov’, ‘krylov-lu’, ‘krylov-mg’, ‘gs’, ‘jacobi’, ‘mg’, ‘null’] |
[‘LinearSolver’] |
Linear solver |
derivative_solver |
krylov |
[‘krylov-dense’, ‘dense-lu’, ‘dense-chol’, ‘lu’, ‘ilu’, ‘krylov’, ‘krylov-lu’, ‘krylov-mg’, ‘gs’, ‘jacobi’, ‘mg’, ‘null’] |
[‘LinearSolver’] |
Linear solver used for computing output derivatives (dy_dyt) |
grad_weight |
0.5 |
None |
[‘Integral’, ‘float’] |
Weight on gradient training data |
solver_tolerance |
1e-12 |
None |
[‘Integral’, ‘float’] |
Convergence tolerance for the nonlinear solver |
nonlinear_maxiter |
10 |
None |
[‘Integral’] |
Maximum number of nonlinear solver iterations |
line_search |
backtracking |
[‘backtracking’, ‘bracketed’, ‘quadratic’, ‘cubic’, ‘null’] |
[‘LineSearch’] |
Line search algorithm |
save_energy_terms |
False |
None |
[‘bool’] |
Whether to cache energy terms in the data_dir directory |
data_dir |
None |
[None] |
[‘str’] |
Directory for loading / saving cached data; None means do not save or load |
max_print_depth |
5 |
None |
[‘Integral’] |
Maximum depth (level of nesting) to print operation descriptions and times |
order |
3 |
None |
[‘Integral’, ‘tuple’, ‘list’, ‘ndarray’] |
B-spline order in each dimension - length [nx] |
num_ctrl_pts |
15 |
None |
[‘Integral’, ‘tuple’, ‘list’, ‘ndarray’] |
# B-spline control points in each dimension - length [nx] |
Options (RMTC)¶
Option |
Default |
Acceptable values |
Acceptable types |
Description |
|---|---|---|---|---|
print_global |
True |
None |
[‘bool’] |
Global print toggle. If False, all printing is suppressed |
print_training |
True |
None |
[‘bool’] |
Whether to print training information |
print_prediction |
True |
None |
[‘bool’] |
Whether to print prediction information |
print_problem |
True |
None |
[‘bool’] |
Whether to print problem information |
print_solver |
True |
None |
[‘bool’] |
Whether to print solver information |
xlimits |
None |
None |
[‘ndarray’] |
Lower/upper bounds in each dimension - ndarray [nx, 2] |
smoothness |
1.0 |
None |
[‘Integral’, ‘float’, ‘tuple’, ‘list’, ‘ndarray’] |
Smoothness parameter in each dimension - length nx. None implies uniform |
regularization_weight |
1e-14 |
None |
[‘Integral’, ‘float’] |
Weight of the term penalizing the norm of the spline coefficients. This is useful as an alternative to energy minimization when energy minimization makes the training time too long. |
energy_weight |
0.0001 |
None |
[‘Integral’, ‘float’] |
The weight of the energy minimization terms |
extrapolate |
False |
None |
[‘bool’] |
Whether to perform linear extrapolation for external evaluation points |
min_energy |
True |
None |
[‘bool’] |
Whether to perform energy minimization |
approx_order |
4 |
None |
[‘Integral’] |
Exponent in the approximation term |
solver |
krylov |
[‘krylov-dense’, ‘dense-lu’, ‘dense-chol’, ‘lu’, ‘ilu’, ‘krylov’, ‘krylov-lu’, ‘krylov-mg’, ‘gs’, ‘jacobi’, ‘mg’, ‘null’] |
[‘LinearSolver’] |
Linear solver |
derivative_solver |
krylov |
[‘krylov-dense’, ‘dense-lu’, ‘dense-chol’, ‘lu’, ‘ilu’, ‘krylov’, ‘krylov-lu’, ‘krylov-mg’, ‘gs’, ‘jacobi’, ‘mg’, ‘null’] |
[‘LinearSolver’] |
Linear solver used for computing output derivatives (dy_dyt) |
grad_weight |
0.5 |
None |
[‘Integral’, ‘float’] |
Weight on gradient training data |
solver_tolerance |
1e-12 |
None |
[‘Integral’, ‘float’] |
Convergence tolerance for the nonlinear solver |
nonlinear_maxiter |
10 |
None |
[‘Integral’] |
Maximum number of nonlinear solver iterations |
line_search |
backtracking |
[‘backtracking’, ‘bracketed’, ‘quadratic’, ‘cubic’, ‘null’] |
[‘LineSearch’] |
Line search algorithm |
save_energy_terms |
False |
None |
[‘bool’] |
Whether to cache energy terms in the data_dir directory |
data_dir |
None |
[None] |
[‘str’] |
Directory for loading / saving cached data; None means do not save or load |
max_print_depth |
5 |
None |
[‘Integral’] |
Maximum depth (level of nesting) to print operation descriptions and times |
num_elements |
4 |
None |
[‘Integral’, ‘list’, ‘ndarray’] |
# elements in each dimension - ndarray [nx] |